Suppose you have a plain cube and you are interested to paint it using "n" colours (not necessary to use all the colours) in such a way that no two adjacent faces of the cube have same colour (Two faces are adjacent if they share a common edge). Two colouring configurations are considered the same if one can be obtained by rotation of the other. Find the number of distinct ways to colour the cube.
Try it out yourself for atleast 30 minutes and then scroll down for hints...
Pair up the opposite faces of the cube into three pairs, say 
. For example, 
. We do this because the only two faces that are not adjacent are the opposite faces and hence only they can be coloured with the same colour.
So, we need at least 
colours of paint with each colour to each of the pairs 
so that no adjacent faces have the same colour. So, for 
, the number of ways is 
. For 
, try to find it casewise on the number of colours that is actually painted on the cube...
Case 1: We use exactly colours to paint, say 
Number of ways to choose those colours 
and after choosing them, we need to paint each of them to each of the pairs , one of which can be 
, and there is only one way to paint all these because any two of the opposite pairs of faces can be interchanged by a corresponding rotation making them identical. So, there are 
ways to paint in total.
Case 2: We use exactly 
colours to paint, say 
Number of ways to choose those colours 
and after choosing them, let us for instance say that the painting configuration is 
. Then, notice that all the colouring configurations with 
and 
and 
as the colours of opposite faces can be obtained by an appropriate rotation of our original configuration. This is because any two of the opposite pairs of faces can be interchanged by a corresponding rotation and the colours can also be interchanged. So, the number of possible distinct configurations in this choice of colours would be the number of ways to choose two of the colours for colouring one pair of opposite faces which is 
ways. Hence, totally there are 
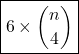ways.
Case 3: We use exactly 
colours to paint, say 
Number of ways to choose those colours 
and an example for the painting configuration could be 
. Even here, all the configurations with 
and 
and as the colours of opposite faces can be obtained by corresponding rotation. So, the total number of possible colourings for this choice will be the number of ways to pair up the colours which would be 
ways. So, totally there are 
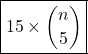ways.
Case 4: We use exactly 
colours to paint, say 
Number of ways to choose those colours 
. After choosing the colours, we have 
ways to paint the faces of the cube (as there are distinct faces of cube) but some of them are identical as they can be obtained from other by rotation. Notice that each colour configuration will give rise to exactly 
paintings ( face colours with ways to position each face onto another face 
) by rotation in those ways including itself. Hence, we divide by to get the number of distinct colour configurations for this choice 
ways. So, totally there are 
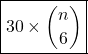ways.
Hence, the total number of ways to paint the cube with 
colours such that no two adjacent faces have same colour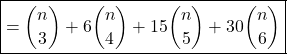 
. Note that the value of 
with 
is considered as in this expression.
Think about the same colouring problem for an Octahedron shown below and write out your ideas and solution in the comments below and the best comment will get rewards from the SuMON math!
Join us at the SuMON Math program to solve more problems like this every fortnight (bi-weekly). We send out detailed solution of the worksheet as hardcopy at your doorstep.
