The question is simple! Consider a ![]() square grid which is divided into unit squares as shown. Find the number of squares whose vertices are these grid points. (one such square is shown)
square grid which is divided into unit squares as shown. Find the number of squares whose vertices are these grid points. (one such square is shown)
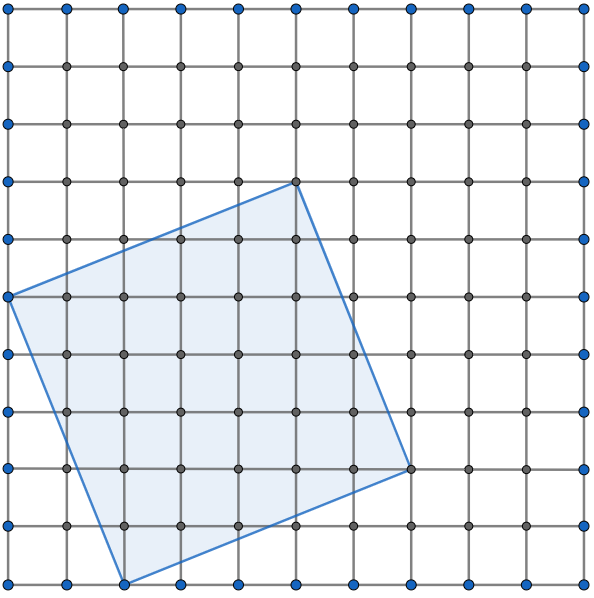
Think on it for sometime (at least ![]() minutes) and then scroll down for more ideas...
minutes) and then scroll down for more ideas...
Call a square "para" if its sides are parallel to the grid lines. A square is said to be "fitted" into another square if its all ![]() vertices lie on all
vertices lie on all ![]() sides of the other square. Can you think of tilted squares as being fitted into some para square? Think about the total number of squares that can be fitted into para squares of various sizes and then scroll down for more ideas...
sides of the other square. Can you think of tilted squares as being fitted into some para square? Think about the total number of squares that can be fitted into para squares of various sizes and then scroll down for more ideas...
Shown below is a ![]() para square with all possible tilted squares fitted into it
para square with all possible tilted squares fitted into it
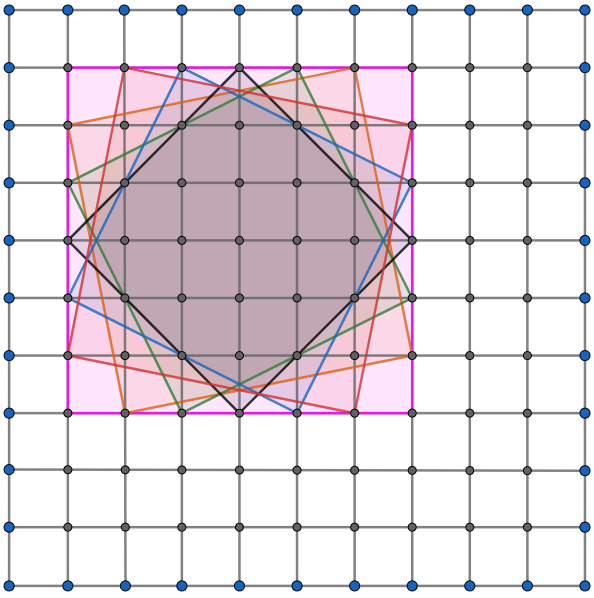
We can observe that there are a total of ![]() squares that can be fitted into a
squares that can be fitted into a ![]() para square. Now, what is the total number of squares that can be fitted into a
para square. Now, what is the total number of squares that can be fitted into a ![]() para square? After finding this value, you need to think about the number of para squares of each size in the
para square? After finding this value, you need to think about the number of para squares of each size in the ![]() grid and multiply it with the corresponding number of squares that can be fitted into each of it.....
grid and multiply it with the corresponding number of squares that can be fitted into each of it.....
For example, the number of para squares of size ![]() (i.e.,
(i.e., ![]() straight squares) would be
straight squares) would be ![]() (which can be counted easily by considering the possibilities for its left-bottom corner). Now, I will leave the task for the reader to find the number of para squares of all other types and put those values in the comments !
(which can be counted easily by considering the possibilities for its left-bottom corner). Now, I will leave the task for the reader to find the number of para squares of all other types and put those values in the comments !
Hence, by multiplying each of it with the number of squares that can be fitted into corresponding para square and taking the sum, we get the total number of squares inside the ![]() grid to be
grid to be ![]() (The calculations are left to the reader).
(The calculations are left to the reader).
There are many other ways to solve this problem. Think about the answer to the same problem for a general ![]() square grid. Comment out your own ideas and answers to the problem and the best comment will get rewards from the SuMON math. Join us at the SuMON Math program to solve more problems like this every fortnight (bi-weekly). We send out detailed solution with the worksheet as hardcopy at your doorstep.
square grid. Comment out your own ideas and answers to the problem and the best comment will get rewards from the SuMON math. Join us at the SuMON Math program to solve more problems like this every fortnight (bi-weekly). We send out detailed solution with the worksheet as hardcopy at your doorstep.
What you've written echoes deeply — like a voice carried through a peaceful valley of thought. Reading this is pure joy and a true inner journey.
Thank you so much. We have written several other blogs. Kindly have a look at it and let us know your thoughts.